Het demystificeren van algoritmes in de praktijk
Er is veel maatschappelijk debat over het gebruik van algoritmes. De Algemene Rekenkamer roept in haar recente rapport daarom op tot demystificatie van deze technieken. Aan de hand van de mogelijkheden van het toepassen van algoritmes in de praktijk, draag ik hier graag mijn steentje aan bij. In dit artikel leg ik uit hoe een Random Forest werkt, en hoe dat bijvoorbeeld van waarde kan zijn voor het onder controle brengen van de schuldenproblematiek door gemeenten.
In de schuldhulpverlening door gemeenten zou het gebruik van algoritmes van grote waarde kunnen zijn. Algoritmes zijn namelijk in staat om op basis van het doorspitten van grote hoeveelheden data te voorspellen wie er mogelijkerwijs behoefte gaat krijgen aan een schuldhulpverleningstraject. Dat is van grote waarde, want hoe eerder problematische schulden worden aangepakt hoe groter de kans op succes.
Tegelijkertijd roept het inzetten van algoritmes bij veel mensen onzekerheden en vraagstukken op. Hoe weet een algoritme of ik al dan niet in de schulden kom? Werkt dit niet stigmatiserend? Hoe werken algoritmes nu eigenlijk precies? Deze laatste vraag is helemaal actueel nu de Algemene Rekenkamer op 26 januari een rapport heeft uitgebracht met de titel ‘Aandacht voor algoritmes’. Een van de aanbevelingen die in dat rapport wordt gedaan is om de burger meer inzicht te geven in de werking van algoritmes. Oftewel, demystificeer algoritmes. Die handschoen pak ik graag op.
Stel je een fictieve gemeente voor van 100 duizend inwoners. Deze gemeente wil voorspellen wie van haar burgers de komende jaren mogelijk in aanmerking komen voor schuldhulpverlening. Dat is belangrijk omdat het vroegtijdig onderkennen van schuldproblematiek dé belangrijke voorwaarde is voor succesvol ingrijpen. Een algoritme dat hiervoor heel goed te gebruiken is, luistert naar de bijna sprookjesachtige naam Random Forest. En alleen al door die naam een goede kandidaat voor demystificatie lijkt me.
Beslisboom
Hoe werkt zo’n Random Forest? Dit algoritme maakt onderdeel uit van een grote groep van algoritmes die zijn gebaseerd op beslisbomen. En die kennen we allemaal, zoals de beslisbomen in de belastingaangifte die met ja/nee-vragen steeds de volgende stap bepalen. De technische omschrijving van zo’n beslisboom is: een algoritme dat een dataset op basis van steeds één kenmerk steeds verder opdeelt, om te komen tot subgroepen waarvan de leden allemaal tot dezelfde categorie behoren.
Stel je nu ook voor dat onze fictieve gemeente vanuit eerdere schuldhulpverleningstrajecten beschikt over een dataset van 1500 burgers. Steeds is vermeld of deze mensen probleemschulden hadden (100 in totaal) en wat op dat moment hun inkomen en leeftijd was.
Op basis van het inkomen en de leeftijd destilleert een beslisboom perfect wie in deze dataset wel of geen schulden heeft. Dit ziet er visueel als volgt uit:
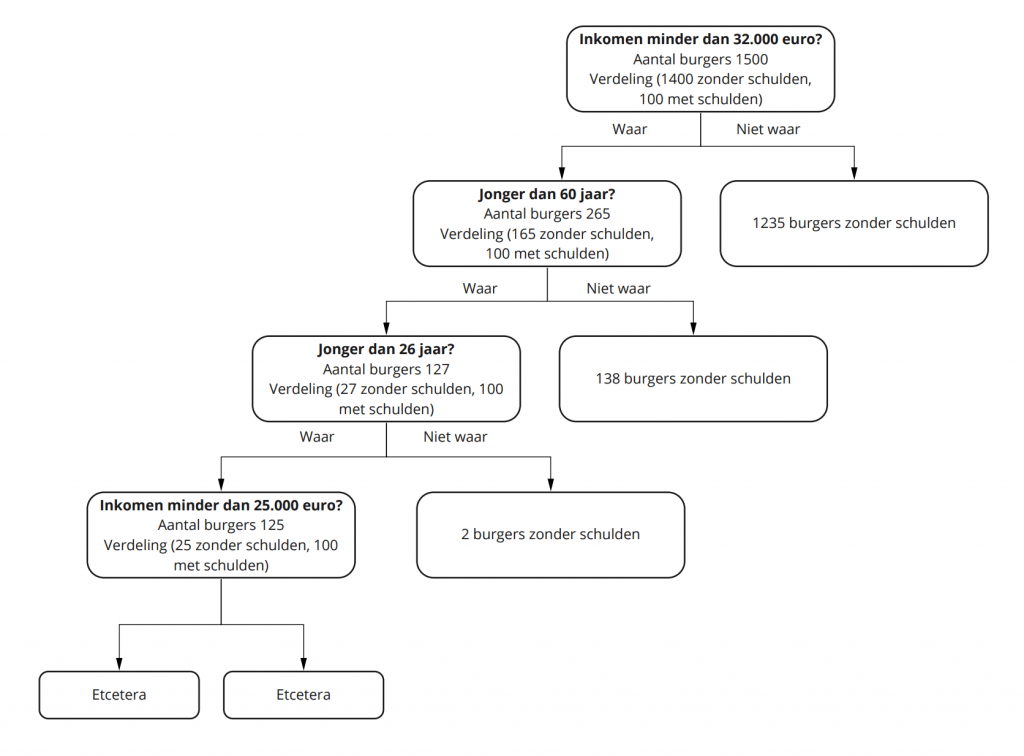
Klik hier om figuur 1 ‘De beslisboom’ te vergroten.
Je weet niet wat je niet weet
Deze beslisboom lijkt misschien waardevol voor het voorspellen van schuldenaren, maar is dat in de praktijk nauwelijks. Want hoe goed deze beslisboom ook voorspelt wie uit de bekende dataset schulden hebben en wie niet, je hebt geen enkele garantie dat deze beslisboom ook in de praktijk kan voorspellen wie in de gemeente als geheel in de probleemschulden komen. De reden hiervoor is dat er in deze gemeente van 100 duizend inwoners hoogstwaarschijnlijk veel meer schuldenaars zullen zijn dan de nu bekende 100 en dat de kans groot is dat deze personen over (net) andere kenmerken beschikken dan de bekende gevallen. Of anders gezegd: omdat deze beslisboom is gebaseerd op één combinatie van kenmerken van de bekende schuldenaren, zal hij niet toekomstige schuldenaren met andere combinaties van kenmerken kunnen voorspellen.
Het Random Forest algoritme lost dit probleem op – de term ‘Forest’ zegt het eigenlijk al – door niet één beslisboom te maken, maar honderden beslisbomen met allerlei kleine variaties die hier gezamenlijk wel de gewenste voorspellende werking hebben. Graag leg ik in wat meer detail uit hoe dat in zijn werk gaat.
De reeds genoemde dataset van 1500 personen wordt eerst opgesplitst. Twee derde van de data (de trainingsdataset) wordt gebruikt voor het maken van de nieuwe beslisbomen, een derde wordt apart gezet (de controledataset) om in een later stadium de resultaten te valideren. Oftewel: hoe goed voorspelt het Random Forest algoritme voor burgers die het algoritme niet eerder gezien heeft?
Vervolgens begint het algoritme op basis van de trainingsdataset steeds nieuwe beslisbomen te maken – in dit geval honderden in totaal – met steeds een andere 2/3 selectie van de beschikbare data per beslisboom. Hierna neemt het algoritme de gemiddelde uitkomst van al deze honderden nieuwe beslisbomen en dat is dan de Random Forest.
Als laatste stap wordt vervolgens gekeken hoe goed deze nieuwe beslisboom, de data uit de apart gezette controledataset voorspelt. In dit geval – figuur 2 – blijkt dat 96 procent te zijn.
In het geval dat de dataset over meer dan twee kenmerken beschikt, maakt het algoritme ook nieuwe beslisbomen door steeds een ander kenmerk achterwege te laten. De voorspellende waarde neemt hierdoor ook verder toe.
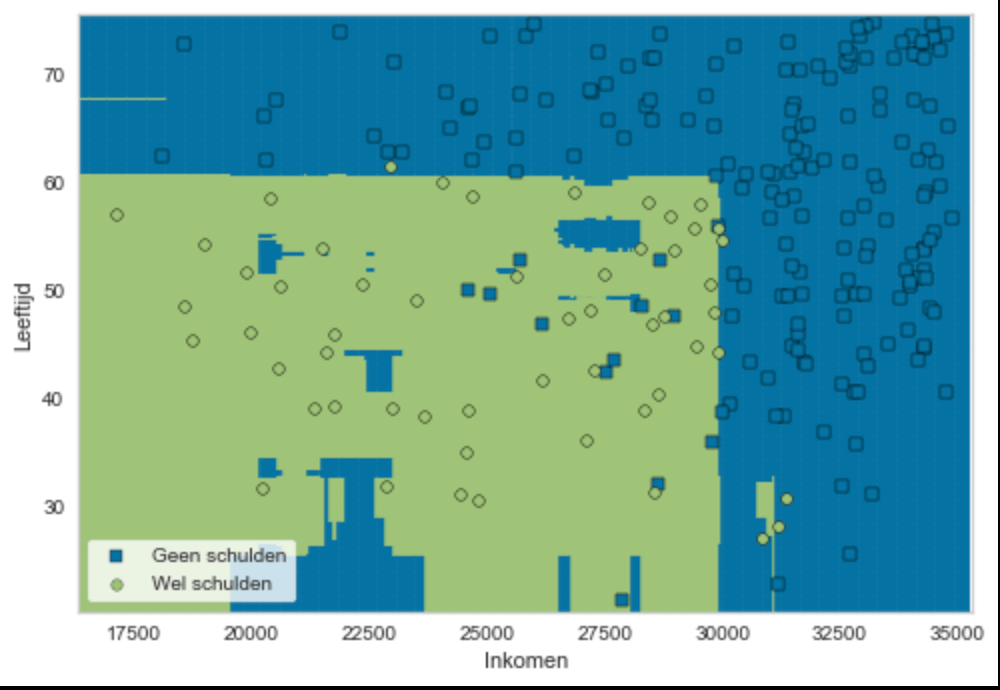
Klik hier om figuur 2 ‘De validatie van de Random Forest’ te vergroten.
De bovenstaande figuur toont de validatie van het Random Forest algoritme van schulden op basis van leeftijd (linkeras) en inkomen (onderste as). De groene vlakken (schulden) en de blauwe vlakken (geen schulden) is de voorspelling van de Random Forest op basis van de trainingsdataset. De groene bolletjes (schulden) en de blauwe vierkantjes (geen schulden) betreffen de 500 personen in de controledataset die het algoritme nog niet eerder had gezien. Te zien valt dat het algoritme de schuldenproblematiek in de controledataset bijna naadloos, namelijk met 96 procent zekerheid, voorspelt.
En juist die mate van toegenomen voorspellende kracht is wat de Random Forest onderscheidt van een enkelvoudige beslisboom. De gemeente weet nu dat zij met het gebruik van dit algoritme slechts 1 op de 25 toekomstige schuldenaren over het hoofd zal zien. Dit terwijl de foutmarge van de oorspronkelijke beslisboom onbekend is, maar hoogstwaarschijnlijk groter is. Deze grote voorspellende kracht wordt door onderzoek in de praktijk bevestigd: bij een vergelijking van 178 algoritmes kwam de Random Forest als beste uit de bus.
Tot slot
Met dit artikel in de hand verdwaalt u hopelijk nooit meer in een Random Forest. In dit artikel heb ik uitgelegd hoe een Random Forest werkt en hoe die in de praktijk zou kunnen worden toegepast met de schuldhulpverlening binnen een gemeentelijke context als voorbeeld. Meer weten hoe u algoritmes als een Random Forest verantwoord, juist en uitlegbaar kunt toepassen op onderwerpen zoals de schuldhulpverlening? Neem contact op via stefan.deblij@vka.nl. Samen kunnen we kijken hoe u maatschappelijke vraagstukken met behulp van algoritmes succesvol aanpakt.
Bronnen
- Delgado et al. (2014). Do we Need Hundreds of Classifiers to Solve Real World Classification Problems? Journal of Machine Learning Research. 15 (2014) 3133-3181.
- Guido, S. & Müller, A.C. (2017). Introduction to Machine Learning with Python: A guide for Data Scientists. O’Reilly.
